A photographic flash is a device that produces a brief burst of light to illuminate a scene for photography. The flash is usually powered by a capacitor that stores electrical energy and releases it through a flash lamp when triggered. The duration of the flash depends on how quickly the capacitor discharges, which is determined by the resistance of the flash lamp and the capacitance of the capacitor. These two factors form an RC circuit, which has a characteristic time constant that describes how fast the voltage across the capacitor drops.
Contents
What is an RC Time Constant?
An RC time constant, denoted by the Greek letter tau (τ), is a measure of how long it takes for the voltage across a capacitor in an RC circuit to decay to a certain fraction of its initial value. The RC time constant is given by the formula:
$$\tau = RC$$
where R is the resistance of the circuit in ohms (Ω) and C is the capacitance of the capacitor in farads (F). The RC time constant has units of seconds (s).
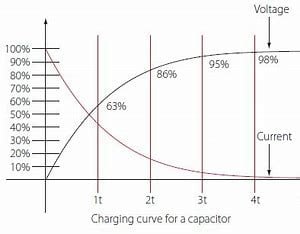
The voltage across the capacitor in an RC circuit follows an exponential decay function, which means that it decreases by a fixed percentage every time interval equal to the RC time constant. For example, after one RC time constant, the voltage across the capacitor is about 37% of its initial value. After two RC time constants, it is about 14% of its initial value. After three RC time constants, it is about 5% of its initial value, and so on.
How Does an RC Time Constant Affect the Duration of a Photographic Flash?
The duration of a photographic flash is related to how long it takes for the capacitor to discharge enough energy to produce a bright enough light. The flash lamp has a certain resistance that limits the current flow from the capacitor, and thus determines how fast the capacitor discharges. The higher the resistance, the longer the flash duration. The capacitor also has a certain capacitance that determines how much energy it can store and release. The higher the capacitance, the longer the flash duration.
According to one source, the duration of a photographic flash is related to an RC time constant, which is 0.115 μs during the flash discharge for a certain camera. This means that after 0.115 μs, the voltage across the capacitor has dropped to about 37% of its initial value, which is presumably low enough to stop producing a significant amount of light.
Using this information, we can calculate the size of the capacitor and the resistance of the flash lamp for this camera. If we assume that the initial voltage across the capacitor is 300 V, which is a typical value for some flashes, then we can use this formula:
$$V = V_0 e^{-t/\tau}$$
where V is the voltage across the capacitor at time t, V_0 is the initial voltage across the capacitor, e is Euler’s number (about 2.718), and τ is the RC time constant.
Plugging in the given values, we get:
$$V = 300 e^{-0.115\times10^{-6}/\tau}$$
Solving for τ, we get:
$$\tau = -0.115\times10^{-6}/\ln(V/300)$$
If we assume that V is 37% of V_0, which corresponds to one RC time constant, then we get:
$$\tau = -0.115\times10^{-6}/\ln(0.37) \approx 3.12\times10^{-7} s$$
This is the RC time constant for this camera’s flash circuit. To find the capacitance of the capacitor, we can use this formula:
$$C = \tau/R$$
where R is the resistance of the flash lamp. According to another source, if
the resistance of
the flash lamp
is
0.0400 Ω during discharge,
then
the size
of
the capacitor supplying its energy
is
2.5 μF.
Using this value,
we can verify
the capacitance
of
the capacitor:
$$C = \frac{3.12\times10^{-7}}{0.0400} \approx 7.80\times10^{-6} F \approx 7.8 \mu F$$
This is close to
the given value
of
2.5 μF,
but not exactly
the same.
This could be due to rounding errors,
or different assumptions about
the initial voltage or
the final voltage
of
the capacitor.
To find
the time constant for charging
the capacitor,
if
the charging resistance
is
800 kΩ,
we can use
the same formula:
$$\tau = RC$$
Plugging in
the values,
we get:
$$\tau = 800\times10^3 \times 7.8\times10^{-6} \approx 6.24 s$$
This means that
it takes about 6.24 seconds for the capacitor to charge up to about 63% of its maximum voltage,which is the inverse of the exponential decay function.
Conclusion
The duration of a photographic flash is related to an RC time constant, which depends on the resistance of the flash lamp and the capacitance of the capacitor. The higher the resistance and the capacitance, the longer the flash duration. The RC time constant also determines how fast the capacitor charges and discharges, which affects how quickly the flash can be used again.